Расчет систем пароснабжения с применением геоинформационных технологий

Расчет систем пароснабжения с применением геоинформационных технологий

Г.Г. Крицкий, кандидат технических наук, доцент, ООО «Политерм»;

Г.Л. Никитин, кандидат физ.-мат. наук, доцент, ООО «Политерм»;

Энергоемкие отрасли промышленности, такие как металлургическая, химическая, бумажная, нефтепереработка и другие потребляют огромное количество пара на производственные нужды. При транспорте и распределении пара из-за разрегулированности систем пароснабжения теряется до 30 % тепловой энергии, в результате чего пар к потребителю поступает с параметрами (температура, давление, влажность), отличающимися от расчетных величин. При этом может происходить снижение качества выпускаемой продукции или нарушение технологического процесса. Для сокращения потерь и увеличения гидравлической и тепловой устойчивости систему пароснабжения периодически налаживают, путем установки на потребителях дросселирующих диафрагм или регуляторов давления. Проведение наладочных работ всегда связано с выполнением соответствующих расчетов.

Все, кто сталкивался с расчетами систем пароснабжения, знают насколько они сложны и трудоемки. Расчету, как правило, подлежали тупиковые сети, транспортирующие перегретый пар одного давления. Сложность выполнения расчетов связана с возможностью возникновения двухфазного состояния теплоносителя (пар, конденсат) и сильной зависимостью параметров, таких как плотность, от температуры и давления. В связи с этим много сил было потрачено на получение простых формул, описывающих сложные физические процессы в системах пароснабжения. Увы, надо признать, что при наличии фазовых переходов, которые часто имеют место в паропроводах, этот подход не привел к успеху. Возникла необходимость в создании более сложных математических моделей, основанных на использовании дифференциальных уравнений.

Развитие вычислительной техники позволяет осуществить качественный скачок в уточнении математических моделей, привлекаемых для расчетов систем пароснабжения, а использование геоинформационных технологий делает удобным ввод данных и анализ результатов расчета.

Стандартный математический аппарат для описания топологии сложной паровой сети, как и для описания других инженерных коммуникаций, это теория графов. Использование систем нелинейных дифференциальных уравнений на графах для описания потерь тепла и давления при транспортировке теплоносителя, в комбинации с уравнениями Кирхгофа, позволяет получить адекватную математическую модель, описывающую процессы, проходящие в паровых сетях. При таком подходе появляется возможность учесть все изменения параметров теплоносителя вдоль каждой трубы, в том числе и изменение фазового состояния. Кроме того, становится возможным выполнить расчет режимов работы не только тупиковых, но и для кольцевых сетей, причем с несколькими источниками пара. Остановимся подробнее на основных моментах описания математической модели.

При движении теплоносителя по паропроводу его параметры (давление, температура и др.) меняются вдоль трубы. Эти изменения связаны с охлаждением теплоносителя через стенку трубы и тепловую изоляцию, а также с потерей давления на трение. Перегретый пар, двигаясь по паропроводу, при определенных условиях может стать влажным (двухфазное состояние теплоносителя), однако температура и давление в этом случае однозначно не определяют его состояние. Удобнее, в качестве динамических переменных выбрать давление и энтальпию. Эти переменные однозначно определяют состояние пара, в том числе температуру и влажность. В общем случае, уравнения, описывающие изменения давления и энтальпии вдоль трубы можно записать в виде:

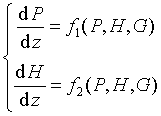
Здесь 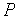– давление (абсолютное), 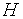– энтальпия (удельное теплосодержание), 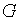– массовый расход, 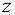– расстояние от начала трубы до текущей точки. Разумеется, переменные 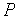и 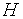зависят от аргумента 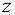, в то время как 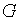, в силу закона сохранения массы, является постоянной величиной для данной трубы и выступает в роли параметра. Конкретный вид функций в правых частях определяется выбором модели, например, будем ли мы учитывать различные режимы течения двухфазной среды: пузырьковый, снарядный и т.д., либо ограничимся моделью гомогенной среды [1].

Для того чтобы из приведенных дифференциальных уравнений найти давление, нужно знать расходы, а чтобы решить алгебраические уравнения Кирхгофа с целью отыскания расходов, нужно знать давления. Выйти из этого «заколдованного» круга, можно, применив метод последовательных приближений, при котором поочередно решаются система алгебраических уравнений, а затем система дифференциальных уравнений.

Начальные условия для дифференциальных уравнений определяются последовательно, начиная с труб, выходящих из источников пара. Для других труб начальные условия для давлений вычисляются из уравнений Кирхгофа, а начальная энтальпия для труб, по которым теплоноситель вытекает из узла, вычисляется как средневзвешенная величина по всем расходам, втекающим в этот узел, причем в качестве весов выступают расходы

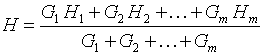
Дифференциальные уравнения можно решать численно, например, методом Рунге-Кутта. Топология паровой сети моделируется с помощью ориентированного графа, причем дуги графа соответствуют участкам труб и элементам, имеющим гидравлическое сопротивление, а вершины графа расположены на концах каждой дуги.

Пусть 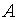– матрица инцидентности (точнее базисная подматрица матрицы инцидентности, которая получается из полной матрицы инцидентности в результате отбрасывания какой-нибудь строки – обычно последней). Тогда, первый закон Кирхгофа, утверждающий, что сумма расходов, втекающих в любой узел и вытекающих из него равна нулю, можно записать в виде матричного уравнения

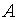
Для записи второго закона Кирхгофа используется матрица базисных циклов 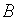. Второй закон Кирхгофа, утверждающий, что сумма падений давления, с учетом действующих напоров, по любому замкнутому контуру равна нулю, можно записать в виде

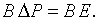
Здесь 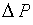– матрица-столбец, составленная из падений давления на каждом из участков трубопроводной сети, 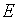– матрица-столбец, составленная из действующих напоров на каждом из участков трубопроводной сети.

Эти уравнения являются нелинейным даже в простейшем случае гидравлической сети, где при решении алгебраических уравнений, может быть использован метод Ньютона. При расчете паропроводов компоненты векторы 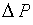определяются из решения системы дифференциальных уравнений, причем решения не являются гладкими функциями. Излом функции образуется в точках перехода теплоносителя от однофазного состояния (перегретый пар) к двухфазному состоянию (появление конденсата) и наоборот. С учетом этих замечаний для решения нелинейных уравнений можно применить метод минимизации невязок. Введем вектор невязок (residual vector) 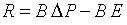, и вычислим норму, например, евклидову (в конечномерном случае все нормы эквивалентны), этого вектора 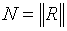. Очевидно, что минимум нормы равен нулю, а решение задачи минимизации совпадает с решением нелинейных уравнений Кирхгофа.

В месте соединения труб могут находиться объекты сети (технологическое оборудование), предназначенные для изменения параметров пара. Например, локальное сопротивление, задвижка, регулятор давления, сепаратор, пароперегревающее устройство, охлаждающий теплообменник, редукционно-охладительное устройство, сопло Вентури, паровая турбина, простой узел. А на концах участков: источник, потребитель либо устройство для сброса пара.

Все эти объекты обладают индивидуальными свойствами, которые следует учитывать при «сшивании» динамических переменных при переходе от одной трубы (входящей в объект), к другой трубе (выходящей из объекта). Ниже приведены условия «сшивания», они же описывают математические модели для перечисленных объектов.

Локальное сопротивление характеризуется только одним гидравлическим сопротивлением . При этом условия сшивания параметров на стыке труб имеют вид

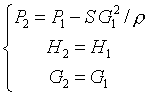
Здесь и далее параметры теплоносителя на входе в объект имеют нижний индекс 1, а на выходе – 2, 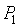– давление на входе в регулятор, 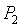– давление на выходе, 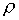– плотность теплоносителя.

Задвижка также характеризуется только одним гидравлическим сопротивлением 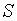. При этом условия сшивания параметров на стыке труб имеют такой же вид, как у локального сопротивления.

Регулятор давления характеризуется давлением 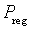, которое требуется получить после регулятора и пропускной способностью 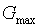, которая позволяет рассчитать минимальное гидравлическое сопротивление регулятора. Если при полностью открытом регуляторе давление после него больше требуемого, то гидравлическое сопротивление регулятора подбирается из условия

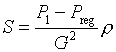
минимальное сопротивление находится по формуле

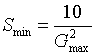
Сепаратор характеризуется гидравлическим сопротивлением 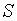и коэффициентом сепарации 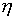(доля конденсата, которая отделяется в результате сепарации смеси пар - конденсат)

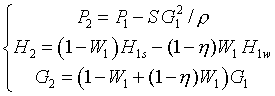
Здесь 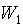– влажность пара на входе в сепаратор, 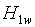– энтальпия воды при температуре насыщения, 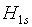– энтальпия сухого пара при температуре насыщения.

Пароперегревающее устройство (ППУ) представляет собой теплообменник, который характеризуется гидравлическим сопротивлением 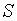и количеством тепла в единицу времени 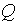(тепловой поток), которое передается пару. Условия сшивания имеют вид

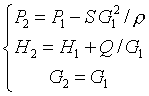
В рамках этой модели можно величину 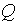задавать явно (1-й тип ППУ) или подбирать из условия равенства выходной температуры заданному значению 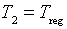(2-й тип ППУ).

Охладитель-теплообменник (ОТО) описывается такой же моделью, что и ППУ, но с отличием в знаке при 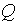. В рамках этой модели, также как и в случае ППУ, величину 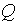можно задавать явно (1-й тип ОТО) или подбирать из условия равенства выходной температуры заданному значению 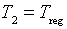(2-й тип ОТО).

Редукционно-охладительное устройство (РОУ) помимо гидравлического сопротивления 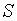характеризуется коэффициентом смешения 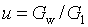(доля подмешиваемой воды по отношению к входящему расходу) и температурой подмешиваемой воды 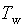. Выходные параметры вычисляются по формулам

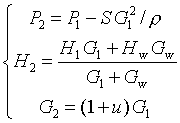
Здесь 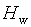– энтальпия подмешиваемой воды, ее легко вычислить из уравнения состояния среды по известным температуре 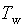и давлению 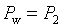. В рамках этой модели можно величину задавать явно (1-й тип РОУ) или подбирать из условия равенства выходной температуры заданному значению 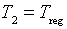(2-й тип РОУ). Для 2-го типа РОУ подбирается и гидравлическое сопротивление из условия равенства давления на выходе заданному значению .

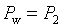Сопло Вентури помимо гидравлического сопротивления 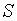характеризуется величиной температура пара на выходе 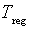, которая поддерживается на нужном уровне с помощью управления величиной расхода 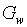подмешиваемой воды

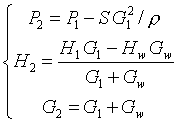
Здесь величина 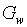подбирается из условия .

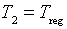Паровая турбина характеризуется двумя параметрами. Первый – давление на выходе из турбины 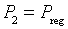, которое поддерживается на нужном уровне с помощью подбора гидравлического сопротивления (первое уравнение)

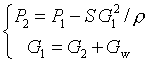
и второй параметр – это один из расходов (в зависимости от режима работы турбины) либо расход пара на входе в турбину 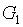(режим 1), либо расход конденсата 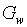(режим 2), отводимого от турбины (оба режима описываются вторым уравнением). Для вычисления энтальпии пара на выходе из турбины полагаем, что процесс в турбине имеет адиабатический характер, поэтому энтальпия вычисляется с привлечением изоэнтропы. Наконец, для учета внутренних потерь энергии в турбине используется к.п.д. 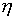, что приводит к некоторому повышению энтальпии

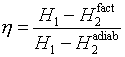
Потребитель моделируется несколькими типами:

• потребитель с «фиксированным» отбором пара;
• потребитель – эжектор;
• потребитель – теплообменник;
• потребитель с заданным гидравлическим сопротивлением.

Узел служит для соединения двух и более труб. Если в узел пар поступает по одной трубе, то давление и энтальпия пара в начале всех выходящих из узла труб будут такие же, как у пара поступающего в узел. Более интересен случай, когда пар поступает в узел по двум или более трубам и имеет различные параметры. Давления в этом случае, разумеется, равны друг другу и эта величина берется в качестве начального условия при решении дифференциальных уравнений для труб, по которым пар выходит из узла. Энтальпия также одинакова в начале этих труб, но равняется средневзвешенному значению энтальпий входящих потоков пара, причем в качестве веса выступает расход

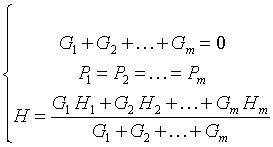
Источник, как правило, характеризуется давлением и температурой, а для начальных условий необходимо знать энтальпию теплоносителя. Если теплоноситель – однофазная среда: сухой пар или, наоборот, теплоносителем является вода, то в этих случаях известные давление и температура позволяют вычислить энтальпию в начале трубы, отходящей от источника, используя уравнения состояния пара и воды. Если же пар является влажным, то нужно знать давление и влажность (температура насыщения при этом однозначно определяется давлением) и тогда опять же можно вычислить энтальпию. В этом случае справедлива формула

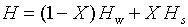
где 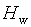– энтальпия воды, 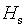– энтальпия насыщенного пара, 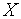– степень сухости пара, 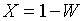, 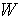– влажность пара.

На основании изложенной методики разработан программно-расчетный комплекс ZuluSteam 5.2, позволяющий выполнять наладочный и поверочный расчеты, как тупиковых, так и кольцевых паровых сетей, работающих от одного или нескольких источников с различными выходными параметрами пара. Ограничений на количество участков и объектов системы пароснабжения нет.

Ниже приводится пример расчета, выполненного с помощью этой программы.

Как видно из рисунка 1, паровая сеть кольцевая и имеет три источника пара различного давления 40, 18 и 9 кг/см2. В этой сети присутствуют все объекты, перечисленные выше.

На рисунке 2 изображены графики изменения давления (синий цвет), температуры (красный), влажности (зеленый) и энтальпии (желтый) вдоль пути, который отмечен на рисунке 1 красными флажками.

Кроме графиков, для анализа режимов работы паровой сети, пользователю предоставляется много другой информации, например:

• Значения давлений, температур, энтальпии и влажности для каждого участка и узла паровой сети.
• Расход и средняя скорость движения теплоносителя на участках.
• Расстояние от начала участка до точек начала и окончания конденсации.
• Список потребителей, у которых не выдерживаются заданные параметры давления, температуры и влажности.

С помощью геоинформационной системы, используя запросы, можно быстро найти или выбрать любую требуемую информацию о параметрах и режиме работы паровой сети, а также распечатать отчет, включающий таблицы, графики и текстовые сообщения.

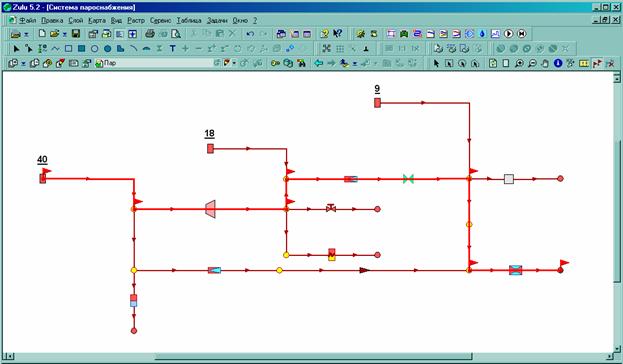
Рисунок 1

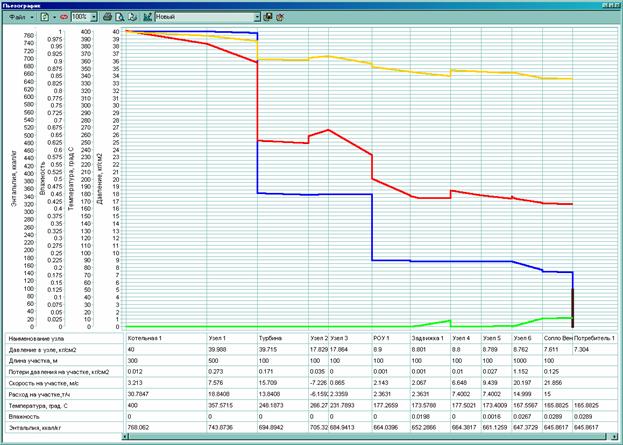
Рисунок 2

Литература

1. Кириллов П.Л., Юрьев Ю.С., Бобков В.П. Справочник по теплогидравлическим расчетам (ядерные реакторы, теплообменники, парогенераторы), М., Энергоатомиздат, 1990.