Гидравлические расчеты газовых сетей
Г.Г. Крицкий, кандидат технических наук, доцент, ООО «Политерм»;
Г.Л. Никитин, кандидат физ.-мат. наук, доцент, ООО «Политерм»;
Выбрать математическую модель для расчета режимов работы газовой сети сравнительно легко, есть достаточное количество специальной литературы, например, монография Ионина А.А. [1].
Однако для большинства специалистов основными документами, которыми они руководствуются при расчете газовых сетей, являются СНиП и Свод Правил. Относясь к этим документам с большим доверием, они забывают о том, что и в них могут быть сделаны ошибки.
В данном случае речь идет об ошибках в формулах вычисления падения давления на участке газовой сети. Эти ошибки порой тиражируются из одного нормативного документа в другой, и на них мало, кто обращает внимание. На наш взгляд, этому способствует несколько обстоятельств:
- Формулы, приведенные в СП, очень похожи на правильные;
- Использование нестандартных единиц измерения и неинвариантная форма записи расчетных выражений затрудняют их анализ.
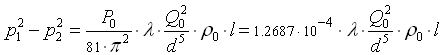 (1.1)
(1.1)
В формуле (1.1) и далее по тексту будут использованы следующие обозначения:
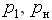 - давление в начале трубы;
- давление в начале трубы; 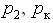 - давление в конце трубы;
- давление в конце трубы;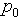 - стандартное атмосферное давление;
- стандартное атмосферное давление;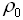 - плотность газа при нормальных условиях (при атмосферном давлении и температуре 0 );
- плотность газа при нормальных условиях (при атмосферном давлении и температуре 0 );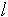 - длина трубы;
- длина трубы;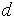 - внутренний диаметр трубы;
- внутренний диаметр трубы;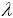 - коэффициент гидравлического трения.
- коэффициент гидравлического трения.
Анализируя формулу (1.1) следует заметить, что она приведена в СП без учета требований нормативных документов, которые предписывают, все единицы измерения физических величин представлять в международной системе СИ. Отсюда метры кубические и сантиметры в пятой степени в одной формуле.
Использование несистемных единиц и замена абсолютных безразмерных констант на приближенные коэффициенты приводит к погрешностям при выполнении расчетов.
Анализ формулы (1.1) начнем с простого вопроса: Какое количество цифр нужно удерживать в промежуточных вычислениях, если в ответе хотим получить пять «верных» значащих цифр?
Ответ - минимум 6. При этом в случае большого количества промежуточных значений, погрешности могут накапливаться. Если в вычислениях имеет место вычитание близких по величине чисел, то количество цифр удерживаемых в промежуточных вычислениях может быть и больше 6.
В связи с этим, в какой степени можно доверять коэффициенту 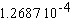 в правой части формулы (1.1)? Простые вычисления показывают, что этот коэффициент получен при удержании в числе
в правой части формулы (1.1)? Простые вычисления показывают, что этот коэффициент получен при удержании в числе 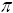 трех значащих цифр 3.14. Если бы было взято более точное значение числа, например,
трех значащих цифр 3.14. Если бы было взято более точное значение числа, например, 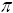 = 3.141592, то коэффициент, имел бы другое значение
= 3.141592, то коэффициент, имел бы другое значение 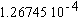 . Таким образом, две последние цифры в коэффициенте ошибочны, хотя погрешность и не велика, ее можно было бы избежать, не вводя в формулу заранее вычисленных коэффициентов. Подобные вопросы, а также действия с приближенными числами, достаточно подробно изложены в [3].
. Таким образом, две последние цифры в коэффициенте ошибочны, хотя погрешность и не велика, ее можно было бы избежать, не вводя в формулу заранее вычисленных коэффициентов. Подобные вопросы, а также действия с приближенными числами, достаточно подробно изложены в [3].
А теперь перейдем к физике. Проанализируем, как в формуле (1.1) вычисляется коэффициент гидравлического трения 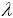 , который, как известно, зависит от числа Рейнольдса. Чтобы зафиксировать проблему, перед теоретическим анализом формул приведем сравнительные вычисления числа Рейнольдса. Классическая формула для его определения приведена в [1].
, который, как известно, зависит от числа Рейнольдса. Чтобы зафиксировать проблему, перед теоретическим анализом формул приведем сравнительные вычисления числа Рейнольдса. Классическая формула для его определения приведена в [1].
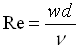 . (1.2)
. (1.2)
где:
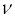 - коэффициент кинематической вязкости газа;
- коэффициент кинематической вязкости газа;
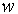 - скорость течения газа.
- скорость течения газа.
Формула, приведенная в СП 42-101-2003, имеет вид:
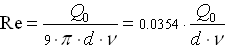 . (1.3)
. (1.3)
Проведем вычисления числа 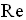 по формулам, приведенным в [1], [2], [5],
по формулам, приведенным в [1], [2], [5],
Параметры газа возьмем из книги [4] пример 1,
Газ - метан, Плотность при нормальных условиях 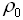 = 0.717
= 0.717 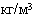 . Объемный расход при нормальных условиях
. Объемный расход при нормальных условиях 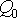 = 13.89
= 13.89 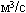 . Давление газа в газопроводе
. Давление газа в газопроводе 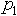 =0.3 МПа, Температура
=0.3 МПа, Температура 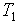 = 373.15
= 373.15 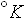 (100
(100 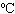 ). Плотность газа
). Плотность газа 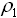 = 1.554
= 1.554 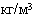 ,
, 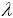 = 0.015. Длина участка газопровода
= 0.015. Длина участка газопровода 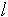 = 500 м. Диаметр участка
= 500 м. Диаметр участка 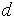 = 0.35 м. Объемный расход при фактических условиях
= 0.35 м. Объемный расход при фактических условиях 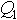 = 6.43
= 6.43 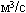 . Скорость движения газа
. Скорость движения газа 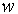 = 66.8 м/с;. Кинематический коэффициент вязкости
= 66.8 м/с;. Кинематический коэффициент вязкости 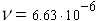 . Результаты вычислений
. Результаты вычислений 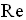 сведены в таблицу 1.
сведены в таблицу 1.
Таблица 1
| Используемая формула | Значение Re |
| Ионин А.А. [1] |
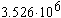
|
| FS Pressure Drop 6.2 [5] |
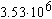
|
| СП 42-101-2003 [2] |
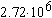
|
Программу FS Pressure Drop 6.2 [5] можно скачать в Интернете и в течение некоторого времени пользоваться ей бесплатно.
Значения, приведенные в таблице 1, показывают, что имеет место расхождение в результатах вычислений. Кроме того, увеличение скорости движения газа на участке в два раза приводит при расчете по [1], [5] к увеличению число Рейнольдса вдвое, а при расчете по формуле из [2] получается то же самое значение. Конечно, при тех скоростях, которые имеют место в газопроводах среднего и высокого давления коэффициент гидравлического трения 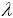 изменится очень незначительно. Однако по нашему мнению, в формуле (1.3) имеет место путаница понятий. Прежде всего, речь пойдет о расходах газа. При транспортировке газообразных сред различают два вида расхода - массовый и объемный. Массовый расход G, размерность кг/с, для которого справедлив закон сохранения (расход не меняется вдоль трубы). Обычно этот расход используется в уравнениях Кирхгофа при увязке потокораспределения. Объемный расход
изменится очень незначительно. Однако по нашему мнению, в формуле (1.3) имеет место путаница понятий. Прежде всего, речь пойдет о расходах газа. При транспортировке газообразных сред различают два вида расхода - массовый и объемный. Массовый расход G, размерность кг/с, для которого справедлив закон сохранения (расход не меняется вдоль трубы). Обычно этот расход используется в уравнениях Кирхгофа при увязке потокораспределения. Объемный расход 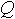 , который в дальнейшем во избежание путаницы будем называть фактическим, объемным расходом. Этот расход обладает большим недостатком, для него не выполняется закон сохранения, т.е. он меняется вдоль трубы с изменением плотности газа. Данный расход вычисляется по формуле
, который в дальнейшем во избежание путаницы будем называть фактическим, объемным расходом. Этот расход обладает большим недостатком, для него не выполняется закон сохранения, т.е. он меняется вдоль трубы с изменением плотности газа. Данный расход вычисляется по формуле 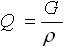 и имеет размерность
и имеет размерность 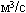 . Фактический объемный расход пропорционален скорости
. Фактический объемный расход пропорционален скорости 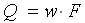 , где
, где 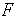 - площадь поперечного сечения трубы (
- площадь поперечного сечения трубы ( 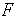 = const). Чтобы избавиться от упомянутого недостатка фактического объемного расхода, в любом учебнике по газоснабжению [1] вводится еще одно понятие объемного расхода
= const). Чтобы избавиться от упомянутого недостатка фактического объемного расхода, в любом учебнике по газоснабжению [1] вводится еще одно понятие объемного расхода 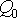 . Этот условный объемный расход вычисляется по формуле
. Этот условный объемный расход вычисляется по формуле 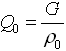 , здесь
, здесь 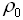 - плотность газа в нормальных условиях, определенная при температуре
- плотность газа в нормальных условиях, определенная при температуре 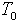 = 0
= 0 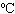 и давлении
и давлении 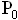 = 0.101325 МПа;
= 0.101325 МПа; 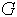 - массовый расход газа.
- массовый расход газа. 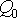 имеет ту же размерность, что и фактический объемный расход, но является совершенно другой физической величиной. Его свойства такие же, как у массового расхода, т.е. он не меняется вдоль трубы, поэтому именно он используется при расчетах поставщиков газа с потребителями. Наличие двух объемных расходов может привести к путанице, что и наблюдается в СП 42-101-2003.
имеет ту же размерность, что и фактический объемный расход, но является совершенно другой физической величиной. Его свойства такие же, как у массового расхода, т.е. он не меняется вдоль трубы, поэтому именно он используется при расчетах поставщиков газа с потребителями. Наличие двух объемных расходов может привести к путанице, что и наблюдается в СП 42-101-2003.
Переходя в формуле (1.2) от скорости к фактическому объемному расходу с учетом того, что 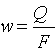 , a
, a 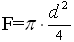 , получим:
, получим:
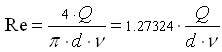 (1.4)
(1.4)
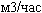 , а диаметр в сантиметрах, как в СП 42-101-2003, то получим:
, а диаметр в сантиметрах, как в СП 42-101-2003, то получим:
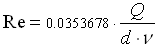 (1.5)
(1.5)
Формула (1.5) при соответствующем округлении множителя совпадает с формулой из СП 42-101-2003 с той лишь разницей, что в числителе в место 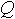 стоит значение
стоит значение 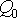 .
.
Нет смысла переходить в общепринятой формуле для определения числа Рейнольдса от скорости к условному объемному расходу - формула будет другая, и будет содержать отношение плотностей.
Впрочем, и без вычислений можно понять, что 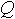 в формуле для числа Рейнольдса может быть только фактическим объемным расходом, поскольку именно эта физическая величина пропорциональна скорости.
в формуле для числа Рейнольдса может быть только фактическим объемным расходом, поскольку именно эта физическая величина пропорциональна скорости.
К сожалению, это не последняя, досадная ошибка сделанная в СП 42-101-2003. Для обнаружения следующей ошибки, сравним результаты вычислений падения давления по трем различным формулам, приведенным в [1], [2], [5]. Формула из [1], без учета коэффициента сжимаемости, имеет вид:
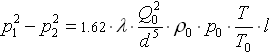 (1.6)
(1.6)
Формула из программы FS Pressure Drop 6.2 [5]
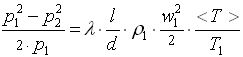 (1.7)
(1.7)
Формула из СП 42-101-2003 (1.1)
Здесь:
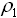 - плотность газа в начале трубы;
- плотность газа в начале трубы;
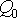 - (условный) объемный расход при нормальных условиях;
- (условный) объемный расход при нормальных условиях;
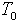 = 273.15
= 273.15 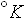 ;
;
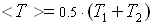 - средняя температура на участке трубопровода;
- средняя температура на участке трубопровода;
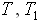 - температура в начале трубы;
- температура в начале трубы;
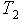 - температура в конце трубы;
- температура в конце трубы;
Для исключения влияния предыдущей ошибки величину гидравлического трения 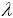 будем брать во всех случаях равной 0.015.
будем брать во всех случаях равной 0.015.
Результаты вычислений падения давления по формулам, приведенным в [1], [2], [5] пример 1, сведены в таблицу 2.
Таблица 2
| Используемая формула | Значение падения давления, МПа |
| Ионин А.А. [1] | 0.0871 |
| FS Pressure Drop 6.2 [5] | 0.0871 |
| СП 42-101-2003 [2] | 0.0606 |
Как видим, имеется существенное расхождение в результатах. Попробуем спасти положение, для этого правую часть в формуле (1.1) умножим на выражение 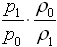 . Новое вычисление дает:
. Новое вычисление дает:
| Используемая формула | Значение падения давления, МПа |
| Исправленная формула СП 42-101-2003 | 0.0871 |
Как видим, ответы по все трем формулам одинаковые. Учитывая, что 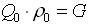 - массовый расход, и
- массовый расход, и 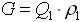 где
где 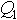 - (фактический) объемный расход, получим "новую" формулу
- (фактический) объемный расход, получим "новую" формулу
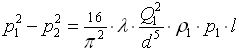 (1.8)
(1.8)
Как не трудно догадаться эта "новая" формула отличается от формулы в СП 42-101-2003 тем, что вместо величин 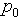 ,
, 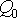 ,
, 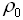 появились
появились 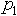 ,
, 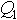 ,
, 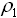 . Почему стоят кавычки у слова новая? Да потому, что эта формула есть ни что иное, как формула из [1], автор Ионина А.А., записанная в других переменных. Чтобы это доказать возьмем формулу из [1] (1.6) и воспользуемся уравнением состояния идеального газа для двух условий
. Почему стоят кавычки у слова новая? Да потому, что эта формула есть ни что иное, как формула из [1], автор Ионина А.А., записанная в других переменных. Чтобы это доказать возьмем формулу из [1] (1.6) и воспользуемся уравнением состояния идеального газа для двух условий 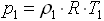 и
и 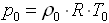 , откуда
, откуда 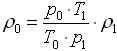 . Кроме того, из равенства
. Кроме того, из равенства 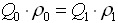 выразим условный объемный расход
выразим условный объемный расход 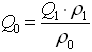 . Подставляя все это в формулу (1.6), получим (1.8), что и не удивительно. Впрочем, гораздо лучше эта формула выглядит в инвариантной форме:
. Подставляя все это в формулу (1.6), получим (1.8), что и не удивительно. Впрочем, гораздо лучше эта формула выглядит в инвариантной форме:
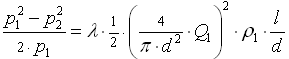 (1.9)
(1.9)
Выражение в скобках - это скорость, и значит, правая часть формулы в точности совпадает с правой частью формулы Дарси-Вейсбаха:
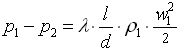 (1.10)
(1.10)
Надеемся, что эти рассуждения убедят Вас в справедливости наших выводов. В заключение хотелось бы пожелать всем авторам не использовать несистемные единицы измерения, не выполнять замену абсолютных безразмерных констант на приближенные коэффициенты, которые могут быть восприняты, как эмпирические значения или как размерные множители.
Литература:
- Ионин А.А. Газоснабжение, М., Стройиздат, 1975.
- Свод правил по проектированию и строительству. Общие положения по проектированию и строительству газораспределительных систем из металлических и полиэтиленовых труб. СП 42-101-2003, М., ЗАО "Полимергаз", 2003
- Щиголев Б.М. Математическая обработка наблюдений, М., Гос. издательство физ.-мат. литературы, 1962.
- Акулов Л.А. и др. Теплофизические свойства крио-продуктов, СПб.: Политехника, 2001.
- http://www.pressure-drop.com
Последнее обновление — 29.06.2015 17:27:08






