Основные этапы построения решения
Дифференциальные уравнения решаются численно методом Рунге-Кутта.
Чтобы выписать уравнения Кирхгофа для произвольной трубопроводной сети целесообразно привлечь теорию графов.
Топология трубопроводной сети моделируется с помощью ориентированного графа, причем дуги графа соответствуют участкам труб и элементам, имеющим гидравлическое сопротивление, а вершины графа соответствуют концам труб (и точкам их соединения).
Пусть A - матрица инцидентности (точнее базисная подматрица матрицы инцидентности, которая получается из полной матрицы инцидентности в результате отбрасывания какой-нибудь строки - обычно последней). Тогда первый закон Кирхгофа, утверждающий, что сумма расходов, втекающих и вытекающих в любой узел равна нулю, можно записать в виде матричного уравнения
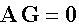
Рисунок 180.
Для записи второго закона Кирхгофа используется матрица базисных циклов В. Эту матрицу можно получить в результате следующей процедуры. Выберем какое-нибудь остовное дерево графа (для ускорения процессов сходимости итерационных процессов решения нелинейных уравнений Кирхгофа рекомендуется выбирать дерево с наименьшим гидравлическим сопротивлением). Выбор остовного дерева (базисного минора матрицы инцидентности) разбивает дуги графа на ветви и хорды, при этом соответствующие расходы разбиваются на базисные и свободные. С учетом этого разбиения уравнение первый закон Кирхгофа можно переписать в виде:
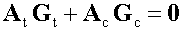
Рисунок 181.
Здесь At и Ac - квадратная и прямоугольная матрицы, составленные соответственно из базисных столбцов (индекс t от английского слова tree - древо) и остальных (индекс с от английского слова chord - хорда).
Выразим базисные переменные через свободные:
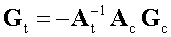
Рисунок 182.
Можно показать, что матрица базисных циклов, соответствующая выбранному остовному дереву имеет вид:
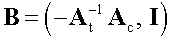
Рисунок 183.
Второй закон Кирхгофа, утверждающий, что сумма падений давления, с учетом действующих напоров, по любому замкнутому контуру равна нулю, можно записать в виде:
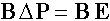
Рисунок 184.
Здесь 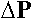 - матрица-столбец, составленная из падений давления на каждом
из участков трубопроводной сети, E матрица-столбец, составленная из действующих
напоров на каждом из участков трубопроводной сети.
- матрица-столбец, составленная из падений давления на каждом
из участков трубопроводной сети, E матрица-столбец, составленная из действующих
напоров на каждом из участков трубопроводной сети.
Уравнение (1.7) является нелинейным даже в простейшем случае гидравлической сети
(в случае гидравлической сети при решении нелинейных уравнений помогает метод
Ньютона). В случае паропроводов компоненты векторы 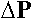 определяются из решения системы дифференциальных уравнений,
причем решения не являются гладкими функциями. Излом решения образуется в точке
появления конденсата. С учетом этих замечаний для решения нелинейных уравнений
применим метод минимизации невязок. Введем вектор невязок (residual vector)
определяются из решения системы дифференциальных уравнений,
причем решения не являются гладкими функциями. Излом решения образуется в точке
появления конденсата. С учетом этих замечаний для решения нелинейных уравнений
применим метод минимизации невязок. Введем вектор невязок (residual vector)
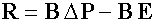
Рисунок 185.
и вычислим норму, например евклидову (в конечномерном случае все нормы эквивалентны), этого вектора:
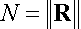
Рисунок 186.