Модель теплообменника
Для расчета больших паропроводных сетей (да и для удобства пользователей) требуется простая математическая модель теплообменника. О существовании такой модели для пароводяных или паровоздушных теплообменных аппаратов нам неизвестно. Поэтому ниже приводится описание разработанной нами модели.
Для построения модели пароводяного теплообменника, сначала создадим модель водоводяного/водовоздушного теплообменника. Для таких теплообменников уже существуют модели, например смотрите Соколов [], но нам нужна такая модель, которую удается обобщить и перенести на случай пар - вода/воздух.
Итак, постановка задачи: в процессе наладочного расчета должна создаваться математическая модель существующего теплообменника по известным данным в одном режиме работы (обычно расчетный/оптимальный, но не обязательно), а в процессе поверочного расчета эта модель будет использоваться для расчета режима работы данного теплообменника при других входных параметрах.
Полагаем, что при наладке известны следующие расчетные (нормативные) параметры
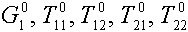 . Ясно, что параметр
. Ясно, что параметр 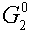 можно вычислить из условия теплового баланса, так для воды:
можно вычислить из условия теплового баланса, так для воды:
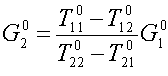
Рисунок 197.
В качестве математической модели естественно взять систему дифференциальных уравнений, описывающих изменение температуры теплоносителей по мере их продвижения внутри теплообменника
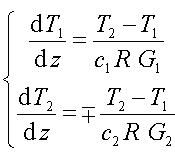
Рисунок 198.
Здесь знак минус, следует выбирать для прямоточных теплообменников, а знак плюс - для противоточных (дальнейшее изложение ведется на примере последних),
-
T1 – температура теплоносителя в первом контуре;
-
T2 – температура теплоносителя во втором контуре;
-
z – относительное расстояние, пройденное теплоносителем внутри теплообменника;
-
c1, с2 – теплоемкости теплоносителей;
-
R – среднее термическое сопротивление перегородки между теплоносителями.
Последний параметр пока неизвестен, и именно он будет отвечать за все отличия одного теплообменника от другого.
Исходных данных 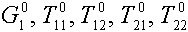 как раз хватает, чтобы задать начальные условия
как раз хватает, чтобы задать начальные условия 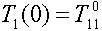 и
и 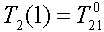 для дифференциальных уравнений и вычислить среднее термическое
сопротивление перегородки между теплоносителями.
для дифференциальных уравнений и вычислить среднее термическое
сопротивление перегородки между теплоносителями.
Отметим, что предлагаемая модель точна для теплообменников типа труба в трубе и аналогичных, поскольку в этом случае термическое сопротивление не меняется вдоль трубы и совпадает со средним (краевыми эффектами для достаточно длинной трубы можно пренебречь).
Решение дифференциальных уравнений имеет вид:
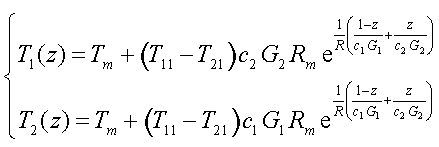
Рисунок 199.
где
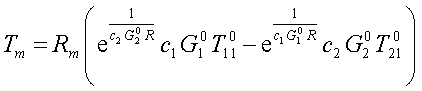
Рисунок 200.
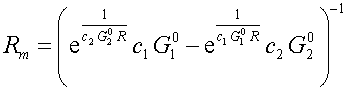
Рисунок 201.
Из уравнения 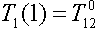 находим среднее термическое сопротивление:
находим среднее термическое сопротивление:
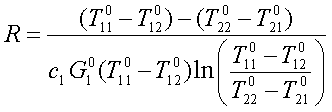
Рисунок 202.
На этом построение математической модели теплообменника завершено и выходные величины
можно вычислить по формулам 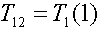 и
и 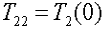 .
.
Пароводяной теплообменник
В этом случае возможно появление фазовых переходов, а для двухфазной среды в качестве динамической переменной (в каждом контуре) естественно выбрать энтальпию H1 и H2 (удельное теплосодержание). Последняя при заданном давлении позволяет вычислить и температуру и степень сухости пара. Поэтому дифференциальные уравнения примут вид:
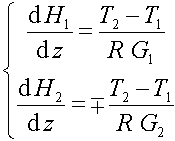
Рисунок 203.
Параметры пара сильно зависят от давления, поэтому следует учесть изменение давления и пополнить список исходных данных при наладке.
Наконец, чтобы система уравнений стала полной нужно использовать уравнения состояния пара и воды.
Далее, ввиду того, что дифференциальные уравнения стали нелинейными, явные формулы получить невозможно. Тем не менее, привлекая численные методы решения дифференциальных и алгебраических уравнений, можно изложенный выше для воды алгоритм реализовать и для пара.